Sei C ein Constraint mit den Variablen
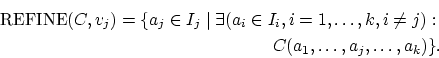
Zur Einschränkung von Intervallgrenzen adaptierte Ernest Davis auf intervallarithmetischen Grundlagen den Waltz-Algorithmus zur Filterung ungültiger Werte aus den Domänen der Constraint-Variablen. Davis (1987) nennt den Effekt Label Inference und bezeichnet damit das sukzessive Ableiten von Wertebereichseinschränkungen und das Belegen der Variablen bzw. Knoten im Constraint-Netz mit der Menge der jeweils möglichen Werte (engl. interval labeling).
Davis (1987) definiert für den Vorgang des Einschränkens der Intervallgrenzen, auch (engl.) label refinement genannt, eine Funktion REFINE, die innerhalb der REVISE-Prozedur des Waltz-Algorithmus (siehe Abbildung 5.23) aufgerufen wird (vgl. Davis, 1987, S. 285):
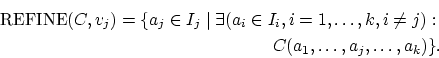
Der Aufruf REFINE![]() liefert somit die Menge der
Werte für
liefert somit die Menge der
Werte für ![]() , die konsistent mit dem Constraint C und
allen anderen Wertebereichen
, die konsistent mit dem Constraint C und
allen anderen Wertebereichen ![]() sind. Ein Wert
sind. Ein Wert ![]() befindet sich
in dieser Ergebnismenge, wenn er in
befindet sich
in dieser Ergebnismenge, wenn er in ![]() ist und Teil des
k-stelligen Tupels
ist und Teil des
k-stelligen Tupels ![]() ist, der das Constraint
ist, der das Constraint
![]() mit den Wertebereichen
mit den Wertebereichen ![]() erfüllt. Eingebettet in die Prozedur
REVISE schränkt diese nun, sofern dies aufgrund des
Constraints
erfüllt. Eingebettet in die Prozedur
REVISE schränkt diese nun, sofern dies aufgrund des
Constraints ![]() möglich ist, mit Hilfe von REFINE der Reihe
nach die Wertebereiche für alle beteiligten Variablen
möglich ist, mit Hilfe von REFINE der Reihe
nach die Wertebereiche für alle beteiligten Variablen
![]() ein, und gibt die Menge der Variablen zurück, deren Wertebereiche sich
geändert haben. Die Ausführung dieser Version des
Waltz-Algorithmus soll an dieser
Stelle durch ein Beispiel erläutert werden
(vgl. Davis, 1987, S. 286 f.):
ein, und gibt die Menge der Variablen zurück, deren Wertebereiche sich
geändert haben. Die Ausführung dieser Version des
Waltz-Algorithmus soll an dieser
Stelle durch ein Beispiel erläutert werden
(vgl. Davis, 1987, S. 286 f.):
![]() wird aus der Warteschlange herausgenommen.
wird aus der Warteschlange herausgenommen.
![]() Da
Da ![]() und
und ![]() , ergibt
, ergibt ![]() für
für
![]() , daher Einschränkung von
, daher Einschränkung von ![]() .
.
![]() Da
Da ![]() und
und ![]() , ergibt
, ergibt ![]() für
für
![]() , daher Einschränkung von
, daher Einschränkung von ![]() .
.
![]() Da
Da ![]() und
und ![]() , ergibt
, ergibt ![]() für
für
![]() , daher Einschränkung von
, daher Einschränkung von ![]() .
.
Weil sich die Wertebereiche von ![]() und
und ![]() geändert haben, wird
geändert haben, wird
![]() zur Warteschlange hinzugefügt.
zur Warteschlange hinzugefügt.
![]() wird aus der Warteschlange herausgenommen.
wird aus der Warteschlange herausgenommen.
![]() Da
Da ![]() , ergibt
, ergibt ![]() für
für ![]() ,
daher Einschränkung von
,
daher Einschränkung von ![]() .
.
![]() Da
Da ![]() , ergibt
, ergibt ![]() für
für ![]() ,
daher Einschränkung von
,
daher Einschränkung von ![]() .
.
Weil sich die Wertebereiche von ![]() und
und ![]() geändert haben, wird
geändert haben, wird
![]() zur Warteschlange hinzugefügt.
zur Warteschlange hinzugefügt.
![]() wird aus der Warteschlange herausgenommen.
wird aus der Warteschlange herausgenommen.
![]() Da
Da ![]() und
und ![]() , ergibt
, ergibt ![]() für
für
![]() , daher Einschränkung von
, daher Einschränkung von ![]() .
.
Weil sich der Wertebereich von ![]() geändert hat,
geändert hat, ![]() allerdings
nirgends außer in
allerdings
nirgends außer in ![]() vorkommt, wird kein weiteres Constraint
zur Warteschlange hinzugefügt.
vorkommt, wird kein weiteres Constraint
zur Warteschlange hinzugefügt.
Aufgrund der nun leeren Warteschlange wird der Algorithmus beendet.
Die Einschränkung der Wertebereiche hat in diesem Fall zu einem
eindeutigen Ergebnis in Form von Punktintervallen geführt:
Dieser frühe Versuch zur Anwendung von Konsistenztechniken und Constraint-Propagation auf kontinuierliche Domänen war allerdings mit erheblichen Problemen behaftet vgl. Davis, 1987, S. 305; Sam-Haroud, 1995, S. 28. So garantiert das eingesetzte Verfahren Konvergenz und Vollständigkeit nur für eingeschränkte Constraint-Klassen. Bei nichtlinearen Constraints ist das Verhalten nicht vorhersagbar und führt (1) häufig zur frühzeitigen Beendigung der Filterung ohne das Konsistenz hergestellt wird (engl. early quiescence), bzw. (2) dass der Prozess in eine Endlosschleife läuft (engl. cycling) oder (3) nur sehr langsam konvergiert und dadurch zu unakzeptablen Antwortzeiten führt (engl. slow convergence).
Davis schlägt mehrere Möglichkeiten vor, dem Problem der Terminierung zu begegnen: Abbruchkriterien könnten z.B. ein Zeitlimit für die Propagation, eine Obergrenze für die Anzahl der Auswertungen einzelner Constraints oder eine Beschränkung der Genauigkeit sein, ab der Intervallgrenzen als identisch angesehen werden (vgl. Davis, 1987, S. 305).
Ein weiteres Manko ist, dass die Anwendung des Waltz-Algorithmus lediglich lokale Konsistenz garantiert, d.h. Konsistenz bezogen auf jeweils ein Constraint, und keine globale Konsistenz, bei der die Wertebereiche der Variablen bzgl. sämtlicher Constraints konsistent sind. Trotzdem ist dieses Verfahren für viele Anwendungen bereits ausreichend, und wurde daher in der Vergangenheit in unterschiedlichen Variationen in einer Reihe von Systemen eingesetzt.