5.2.3.3 Kantenkonsistenz

Ein höherer, lokaler Konsistenzgrad ist die Kantenkonsistenz. Im Gegensatz zur Knotenkonsistenz bezieht sich die Kantenkonsistenz nicht auf die Wertebereiche einzelner Knoten im Constraint-Netz, sondern auf die Domänen der Knoten, die durch eine Kante verbunden sind, d.h. über ein Constraint zueinander in Relation stehen. Für gewöhnlich bezieht sich Kantenkonsistenz aus Gründen der Vereinfachung auf binäre Constraint-Netze.

Kantenkonsistenz stellt sicher, dass die Wertebereiche der Variablen auf die Werte beschränkt werden, die kompatibel zu unmittelbar benachbarten Variablen sind. Zu jedem möglichen Wert einer Variable muss ein passender Wert in den Wertebereichen der Variablen vorhanden sein, die zu dieser Variable über ein Constraint in Relation stehen.^5.15 Formal lässt sich dies wie folgt ausdrücken (vgl. Güsgen, 2000, S. 270):

Definition 5.2.8   (Kantenkonsistenz/arc consistency, AC)
Gegeben sei ein binäres, knotenkonsistentes CSP auf den Variablen $v_1,\ldots,v_n$ mit den Wertebereichen $D_1,\ldots,D_n$. Sei $C_{1,1}^b,\ldots,C_{n,n}^b$ die Menge der binären Constraints im Constraint-Netz, wobei $C_{i,j}^b$, $i,j \in \{1,\ldots,n\}$ und $i \neq j$, die Relation $R_{i,j}^b$ besitzt und die Variablen $v_i$ und $v_j$ einschränkt. Das Constraint-Netz ist kantenkonsistent, falls für alle $i,j \in \{1,\ldots,n\}$ mit $i \neq j$ gilt: $\forall d_i \in D_i$ $\exists d_j \in D_j$ $[(d_i,d_j) \in R_{i,j}^b]$.

Ein Constraint-Netz ist kantenkonsistent, wenn alle Constraints kantenkonsistent sind. Erreicht wird dies, indem Änderungen der Wertebereiche der Constraint-Variablen mittels entsprechender Algorithmen durch das Netz propagiert werden. Alleine durch Herstellung der Kantenkonsistenz kann im Regelfall allerdings keine eindeutige Lösung für ein CSP bestimmt werden, bzw. lässt sich nicht eindeutig feststellen, dass es keine Lösung gibt.

Beispiel 5.2.1   Für das CSP mit den Variablen

$$v_1: \{1,2\}, \quad v_2: \{1,2\}, \quad v_3: \{1,2\}$$

und den Constraints

$$C_{1,2}: v_1 \neq v_2, \quad C_{2,3}: v_2 \neq v_3, \quad C_{1,3}: v_1 \neq v_3$$

gibt es keine eindeutige Lösung, obwohl es Kantenkonsistent ist. Für jede ,,Kante`` bzw. jedes Constraint gibt es für sich genommen mindestens eine lokal konsistente Wertekombination, z.B. $v_1=1$ und $v_2=2$ für $C_{1,2}$. Entsprechend müsste für das Constraint $C_{2,3}$ die Variable $v_3=1$ sein, was aber inkonsistent mit $C_{1,3}$ ist, da $v_1$ ebenfalls 1 ist.

Abbildung 5.3: Propagation zur Herstellung von Kantenkonsistenz

In Abbildung 5.3 ist die zur Erzeugung von Kantenkonsistenz notwendige Propagation anhand des Constraint-Beispiels aus Abschnitt 3.6.3 f. dargestellt. In (a) wird während eines Konfigurierungsvorgangs die Taktfrequenz des Prozessors P_FSB_Rate mit 100 festgelegt. Die Auswertung der Kante bzw. des Constraints $C_1$ bewirkt, dass der Wertebereich von MB_FSB_Rate ebenfalls auf den Wert 100 eingeschränkt wird (b). Die Auswertung des Constraint $C_2$ in (c) schränkt wiederum den Wertebereich von S_FSB_Rate ein. In (d) ist zu sehen, wie durch Auswertung von $C_3$ sichergestellt wird, dass die Wertebereiche von P_FSB_Rate und S_FSB_Rate konsistent mit $C_3$ sind. Da dies der Fall ist, sind keine weiteren Wertebereichseinschränkungen erforderlich. Das Ergebnis der Propagation ist ein kantenkonsistentes Constraint-Netz, welches noch keine eindeutige, allerdings zwei potentielle Lösungen bietet.

Im Folgenden werden einige einfache Algorithmen von Mackworth (1977a) vorgestellt, mit deren Hilfe Kantenkonsistenz erzeugt werden kann. Der in Abbildung 5.4 dargestellte Algorithmus REVISE kann dazu genutzt werden, in knotenkonsistenten, binären Constraint-Netzen zwischen den übergebenen Variablenpaaren $(v_i,v_j) \in D_i \times D_j$ Kantenkonsistenz herzustellen. Erreicht wird dies, indem der Algorithmus sämtliche möglichen Werte $d_i \in D_i$ der ersten Variable daraufhin untersucht, ob es für jeden Wert einen kompatiblen Wert in der Domäne $D_j$ der zweiten Variable gibt. Wenn dies nicht der Fall ist, kann der Wert $d_i$ aus der Domäne $D_i$ gelöscht werden.^5.16 Der Algorithmus REVISE muss auf alle Kanten bzw. binären Constraints angewendet werden. Da er nicht symmetrisch ist, müssen neben den Variablenpaaren $(v_i,v_j)$ ebenfalls die entsprechenden Paare $(v_j,v_i)$ geprüft werden.

Abbildung 5.4: Algorithmus REVISE zur Entfernung inkompatibler Werte (vgl. Mackworth, 1977a, S. 104)

Abbildung 5.5: Der Kantenkonsistenz-Algorithmus AC-1 (vgl. Mackworth, 1977a, S. 104)

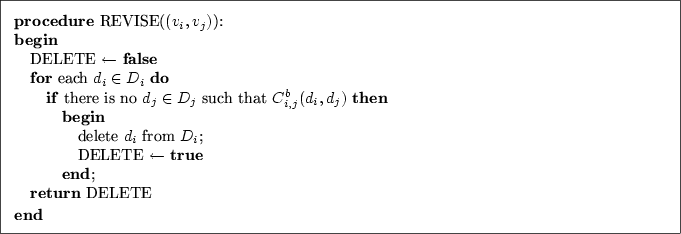Nachdem der Algorithmus auf ein Paar $(v_i,v_j)$ angewendet wurde, ist dieses Variablenpaar zwar kantenkonsistent, bleibt dies aber u.U. nicht. Wenn die Variable $v_j$ ebenfalls zu anderen Variablen durch binäre Constraints in Relation steht, löscht der Algorithmus voraussichtlich aus der Domäne von $v_j$ ebenfalls Werte, so dass anschließend wiederum der Wertebereich von $v_i$ überprüft werden muss, um Kantenkonsistenz zu gewährleisten. Ein einfacher Durchlauf von REVISE ist demnach nicht ausreichend. Stattdessen muss der Algorithmus solange aufgerufen werden, bis keine Änderungen an den Domänen mehr vorgenommen wurden. Erst danach ist die Kantenkonsistenz des Constraint-Netzes sichergestellt. Ein Algorithmus, der diese Funktion übernimmt, ist der in Abbildung 5.5 dargestellte, einfachste Kantenkonsistenz-Algorithmus AC-1. Der Algorithmus AC-1 arbeitet allerdings nicht sehr effizient, da alle Variablenpaare erneut untersucht werden müssen, solange bei einem Durchlauf auch nur eine einzige Änderung an der Domäne einer Variable vorgenommen wurde.

Eine Verbesserung ist der Algorithmus AC-2 (vgl. Mackworth, 1977a, S. 106), der dem von Waltz (1975) beschriebenen Filteralgorithmus entspricht. AC-2 erreicht Kantenkonsistenz mit nur einem einzigen Durchgang der äußeren Schleife durch die Knoten, benötigt dafür allerdings neben Q eine zweite dynamische Liste $Q'$. Aufgrund der Eigenschaften des Algorithmus AC-2 kann es bei Zyklen > 2 im Constraint-Netz dazu kommen, dass eine Kante in beiden Listen Q und $Q'$ gleichzeitig auf Bearbeitung wartet (vgl. Mackworth, 1977a, S. 107). Dies unterschiedet den Algorithmus von dessen Nachfolger AC-3. Der AC-3-Algorithmus (siehe Abbildung 5.6) ist eine Vereinfachung bzw. Verallgemeinerung von AC-2. Er ist nicht mehr darauf ausgelegt, Kantenkonsistenz mit einem einzigen Durchlauf herzustellen. Es wird lediglich eine einzige dynamische Liste Q verwaltet, die wie in AC-1 alle Kanten des Constraint-Netzes enthält.^5.17 Bei Reduzierung des Wertebereichs von $v_k$ durch REVISE müssen alle davon betroffenen Kanten $(v_i,v_k)$ an die Liste Q angefügt werden.^5.18 Dies wird solange wiederholt, bis keine Reduzierung der Wertebereiche mehr erfolgt und die Liste Q vollständig abgearbeitet wurde.

Abbildung 5.6: Der Kantenkonsistenz-Algorithmus AC-3 (vgl. Mackworth, 1977a, S. 106)

Auch der AC-3-Algorithmus ist noch keineswegs optimal. So werden auch durch diesen Algorithmus bei weiteren Durchläufen mit REVISE noch häufig Wertepaare geprüft, von denen bereits bekannt ist, dass sie kompatibel miteinander sind. Eine Reihe von Algorithmen befasst sich damit, diese Metainformationen zu verwalten und durch weniger Konsistenztests effizientere Laufzeiten zu erreichen (siehe Tabelle 5.1). Der AC-4-Algorithmus von Roger Mohr und Thomas C. Henderson nutzt intern eine separate Datenstruktur zur extensionalen Constraint-Repräsentation (vgl. Mohr und Henderson, 1986). Dadurch wird es möglich, REVISE nur für Wertepaare auszuführen, die von einer vorherigen Wertebereichseinschränkung betroffen sind: Ein Wert in einer Domäne gilt als supported, wenn für diesen Wert konsistente Wertebelegungen für alle übrigen Variablen existieren. Wenn in einer Domäne ein Wert gelöscht wird, müssen nicht mehr alle Werte in den Domänen der mit dieser Variablen über ein Constraint verbundenen Variablen getestet werden, sondern nur noch die Werte, die auf den gelöschten Wert über einen support-Eintrag angewiesen waren.

Während also AC-3 bereits nur noch Wertepaare von Kanten prüft, die von Änderungen betroffen sind, reduziert AC-4 nochmals die zu überprüfenden Wertepaare auf diejenigen, die direkt von einer Änderung betroffen sind. Dies resultiert in einer optimalen worst-case Zeitkomplexität, da nicht mehr Konsistenztests als notwendig vorgenommen werden. Allerdings wird diese Verbesserung mit stark erhöhter Platzkomplexität und einer im Durchschnitt dicht am worst-case befindlichen Zeitkomplexität erkauft, so dass der AC-3-Algorithmus in der Praxis häufig performanter als AC-4 arbeitet, trotzdem er das schlechtere worst-case Laufzeitverhalten aufweist vgl. Bessière, 1994a, S. 180; Bessière und Cordier, 1993, S. 108; Wallace, 1993, S. 239 ff..^5.19 Insbesondere in Anwendungen, in denen die Domänen der Constraint-Variablen sehr viele Werte aufweisen, ist aufgrund der erhöhten Platzkomplexität von AC-4 der AC-3-Algorithmus vorzuziehen.

AC-3 und AC-4 gehören zu bisher den am weitesten verbreiteten Algorithmen zur Herstellung von Kantenkonsistenz. Es gibt noch eine Reihe weiterer Algorithmen, die allerdings in der Praxis bisher keine so große Verbreitung gefunden haben. So ist der AC-5-Algorithmus von Pascal Van Hentenryck et al. ein genereller Algorithmus, der sich auf andere Kantenkonsistenz-Algorithmen reduzieren lässt (vgl. Van Hentenryck et al., 1992). AC-3 und AC-4 können als Spezialisierungen von AC-5 gesehen werden. AC-5 besitzt eine besondere Bedeutung für CLP-Sprachen, da sich spezielle, hier vorkommende Klassen von Constraints mittels weiterer Spezialisierungen von AC-5 auf besonders effiziente Weise verarbeiten lassen. AC-5* ist eine Verbesserung von AC-5 in der Hinsicht, dass sich Spezialisierungen nicht nur bzgl. der Zeitkomplexität sondern auch bezogen auf die Platzkomplexität optimieren lassen (vgl. Liu, 1996).

Eine Verbesserung von AC-4 ist der AC-6-Algorithmus von Christian Bessière und Marie-Odile Cordier. AC-6 besitzt bei verringerter Platzkomplexität dasselbe worst-case Laufzeitverhalten wie AC-4 und arbeitet in der Praxis schneller als AC-3 und AC-4. Der AC-6-Algorithmus berechnet für jeden Wert einer Variable zunächst lediglich eine konsistente Wertebelegung pro Constraint. Weitere konsistente Belegungen (bzw. supports) werden erst bei Bedarf erzeugt, d.h. wenn eine vorherige Belegung inkonsistent geworden ist. Die Technik von AC-6 wird deshalb auch lazy oder minimal support genannt (vgl. Bessière und Cordier, 1993; Bessière, 1994a). Weitere Verbesserungen bringt die Berücksichtigung von zusätzlichem Wissen über Constraints, wie die Auswertung von Symmetrieeigenschaften, welches in die Erweiterungen AC-6+ (vgl. Bessière, 1994b) bzw. AC-6++ (vgl. Bessière und Régin, 1995) eingeflossen ist. Die Bemühungen weitere Metainformationen zu berücksichtigen mündeten durch die Arbeiten von von Christian Bessière, Eugene C. Freuder und Jean-Charles Régin in dem Algorithmus AC-7, der bei gleicher Zeit- und Platzkomplexität wie AC-6 durch geschicktes Ausnutzen der Bidirektionalität von Constraints^5.20 weitere Werteüberprüfungen vermeidet (vgl. Bessière et al., 1995,1999a).^5.21

Weil die Datenstrukturen von AC-4, AC-6 und AC-7 zur Vermeidung von doppelten Konsistenztests sehr komplex sind und der Verwaltungsaufwand die Effizienz der Algorithmen in der Praxis vermindert, wurde versucht den Algorithmus AC-3 ohne zusätzliche Datenstrukturen zu verbessern. AC-8 (vgl. Chmeiss und Jégou, 1998,1996b), AC-$3_d$ (vgl. van Dongen, 2002b,a) und AC-2000 (vgl. Bessière und Régin, 2001b,a) sind überarbeitete und leicht verbesserte Versionen von AC-3, die wie der originale Algorithmus ohne aufwendige Datenstrukturen auskommen. Bei gleicher worst-case Komplexität wie AC-3 vermindern sie in der Praxis die Anzahl der benötigten Konsistenztests.^5.22 AC-3.1 (vgl. Zhang und Yap, 2001) und AC-2001 (vgl. Bessière und Régin, 2001b,a) sind Verbesserungen von AC-3, die durch ähnliche Techniken mit sehr einfachen zusätzlichen Datenstrukturen wesentliche Verbesserungen erreichen. AC-3.1 und AC-2001 sind optimale Algorithmen, d.h. sie besitzen eine optimale worst-case Zeitkomplexität, bei gleicher Platzkomplexität wie AC-6 und AC-7.

Die Komplexität von Kantenkonsistenz-Algorithmen ist für den worst-case für binäre Constraints aus theoretischen Gründen auf quadratische Größenordnungen begrenzt. Auch zukünftige Algorithmen können daran nichts ändern. Da mit zunehmendem Grad lokaler Konsistenz, die Komplexität exponentiell anwächst, wird häufig vermieden, einen Konsistenzgrad größer als den der Kantenkonsistenz herzustellen. Ein weiterer Konsistenzgrad allerdings, der für bestimmte Anwendungen eine wichtige Rolle spielt, ist die Pfadkonsistenz.

Fußnoten

...^5.15

Für den allgemeinen Fall der ungerichteten Kantenkonsistenz muss dies auch andersherum gelten.

...^5.16

Dies reduziert nicht die Anzahl der möglichen Lösungen des CSP, da der gelöschte Wert $d_i$ auf keinen Fall zu einer konsistenten Lösung beitragen kann.

...^5.17

Aufgrund der fehlenden Symmetrieeigenschaften von REVISE sowohl die ,,Hin-`` $(v_i,v_j)$ als auch die ,,Rückrichtungen`` $(v_j,v_i)$.

...^5.18

Wobei auf die Rückrichtung $(v_m,v_k)$ der ursprünglichen Kante verzichtet werden kann. Die Kante $(v_m,v_k)$ kann nicht inkonsistent geworden sein, denn durch REVISE wurden aus $D_m$ nur Werte gelöscht, für die es keine korrespondierenden Werte in $D_k$ gibt.

...^5.19

Begründet liegt dies u.a. darin, dass der AC-4-Algorithmus aufgrund von support-Einträgen selektiv ungültige Werte entfernt, während der AC-3-Algorithmus bei jeder Überprüfung eines Constraints sämtliche Werte prüft und so inkonsistente Werte ggf. früher erkennt und entfernt (vgl. Wallace, 1993, S. 242).

...^5.20

Wenn ein Wert von $v_i$ einen Wert von $v_j$ ,,unterstützt``, dann wird ebenso $v_j$ von $v_i$ ,,unterstützt``: Sei $C_{i,j}$, $C_{j,i}$ und $d_i \in D_i$, $d_j \in D_j$, dann ist $C_{i,j}(d_i,d_j)$ gdw. $C_{j,i}(d_j,d_i)$.

...^5.21

Tatsächlich sind die beiden unabhängig voneinander entwickelten Algorithmen AC-6++ von Bessière und Régin (1995) und AC-7 von Freuder (1995) identisch und wurden erstmalig zusammen in demselben Workshop auf der ECAI'94 vorgestellt (vgl. Prosser, 1995b, S. 2).

...^5.22

Wobei für AC-$3_d$, trotzdem dies kein optimaler Algorithmus ist, in Versuchen wesentliche Verbesserungen aufgezeigt wurden. AC-$3_d$ nutzt ebenfalls wie AC-7 die Bidirektionalität von Constraints zur Vermeidung von unnötigen Werteüberprüfungen. Dabei arbeitet AC-$3_d$ weiterhin auf derselben Datenrepräsentation wie der AC-3-Algorithmus.