5.3.4.1 Lokale Toleranzpropagation

Ähnlich der Kantenkonsistenz für finite Domänen definiert Hyvönen einen lokalen Konsistenzgrad für die TP (vgl. Hyvönen, 1992, S. 77):

Definition 5.3.10   (lokal konsistente Toleranzsituation)
Eine Toleranzsituation ist lokal konsistent, gdw. alle Variablen $v_i$, $i \in \{1,\ldots,n\}$ lokal konsistent sind, d.h. für alle Constraints $C_j$, $j \in \{1,\ldots,m\}$ gilt, dass für jede in $C_j$ vorkommenden Variablen $v_i$ zu jeder zulässigen Belegung ${v_i=x}$, ${x \in I_i}$ jeweils eine gültige Belegung der übrigen in $C_j$ vorkommenden Variablen existiert, so dass $C_j$ erfüllt ist.

Während Davis (1987) eine spezielle Funktion REFINE definiert, welche die Constraints im Ganzen propagiert und daher in dieser Form, abhängig von der Implementierung, jeweils nur bestimmte Constraint-Arten verarbeiten kann, basiert die TP auf dem Konzept der solution functions. Dies beruht darauf, dass jede Gleichung eine Menge von Funktionen impliziert. Ein Constraint $C_j$, welches die Variablen $v_{j_1},\ldots,v_{j_k}$ mit $k \leq n$ enthält, ergibt die folgenden Funktionen:

$$\begin{eqnarray*} v_{j_1} & = & F_{j_1}(v_{j_2},\ldots,v_{j_k}) \\ v_{j_2} & = ... ...\vdots & \\ v_{j_k} & = & F_{j_k}(v_{j_1},\ldots,v_{j_{(k-1)}}) \end{eqnarray*}$$

Beispiel 5.3.7   Die impliziten Funktionen bzw. ,,solution functions`` für das einfache Additions-Constraint $C_{1,2,3}: v_1+v_2=v_3$ lauten:

$$\begin{eqnarray*} v_1 = F_1(v_2,v_3) = v_3-v_2 \\ v_2 = F_2(v_1,v_3) = v_3-v_1 \\ v_3 = F_3(v_1,v_2) = v_1+v_2 \end{eqnarray*}$$

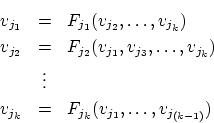
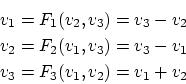
Ein k-stelliges Constraint $C_j(v_{j_1},\ldots,v_{j_k})$ besitzt k implizite Funktionen, je eine für jede Variable $v_{j_i}$, $i \in \{1,\ldots,k\}$. Die Konsistenzbedingungen von $C_j$ sind dann erfüllt, wenn alle impliziten Funktionen erfüllt sind. Anstatt der ursprünglichen Constraints werden daher bei der TP die solution functions ausgewertet und propagiert (vgl. Hyvönen, 1989, S. 1195). Da es bei komplexeren Gleichungen schwierig und teilweise unmöglich ist,^5.97 implizite Funktionen anzugeben, nimmt Hyvönen zunächst eine Vereinfachung des Gleichungssystems durch Zerlegung der Constraints in primitive Constraint-Ausdrücke vor. Teile von komplexen Ausdrücken werden dabei durch Einführung neuer Variablen in zusätzliche Gleichungen überführt. Diese Substitution führt dazu, dass implizite Funktionen leicht erkennbar werden.

Beispiel 5.3.8   Das ICSP mit dem Constraint

$$\begin{eqnarray*} C_1: v_1^3 + v_2 \times v_3 = -v_4 \end{eqnarray*}$$

ist äquivalent zu dem vereinfachten ICSP bestehend aus den folgenden primitiven Constraints:

$C_1: v_5 = v_1^3$	$C_3: v_7 = -v_4$
$C_2: v_6 = v_2 \times v_3$	$C_4: v_7 = v_5 + v_6$

Durch die Einführung neuer Variablen und Termsubstitutionen müssen bei der Propagation ausschließlich primitive Constraint-Ausdrücke behandelt werden, die maximal drei Variablen beinhalten. Dies erleichtert wesentlich die Erstellung der zur Propagation benötigten solution functions.

Hyvönen (1992) bietet durch die lokale TP mit intervallwertigen solution functions einen flexibleren Ansatz als Davis (1987), ist dem Waltz-Filteralgorithmus aber trotzdem sehr ähnlich: Lokale TP stellt lokale Konsistenz her, d.h. Korrektheit ist gewährleistet, es gehen keine vorhandenen Lösungen verloren (wenn es welche gibt, befinden sie sich in den Lösungsintervallen). Allerdings ist das Verfahren ebenfalls unvollständig, da nicht garantiert ist, dass es Lösungen gibt, auch wenn die lokale TP keine (lokale) Inkonsistenz feststellen konnte. Lediglich wenn mittels lokaler TP eine Inkonsistenz aufgefunden wird, kann mit Bestimmtheit gesagt werden, dass keine (globale) Lösung existiert.

Fußnoten

...^5.97

Beispielsweise $x+\log(x)=0$.