5.3.7.1 Konsistenz durch $2^k$-Bäume

Sam-Haroud und Faltings setzen die Anwendung von totalen Constraints voraus, d.h. sämtliche Relationen bzgl. einer Menge von Variablen werden jeweils in einem einzigen Constraint zusammengefasst (vgl. Definition 4.1.2). In Bezug auf $2^k$-Bäume gestaltet sich diese Berechnung einfach, da lediglich die einzelnen $2^k$-Bäume erstellt und hiervon die Schnittmenge gebildet werden muss (vgl. Sam-Haroud und Faltings, 1996a, S. 95). Der resultierende Baum beschreibt den Lösungsraum des benötigten totalen Constraints. In Abbildung 5.27 ist beispielhaft dargestellt, wie ein $2^k$-Baum generiert wird:

Beispiel 5.3.10   Die beiden Constraints aus Abbildung 5.27(a) bilden zusammen die Relation $R_{1,2}$, die den Lösungsraum für $v_1$ und $v_2$ beschreibt. Da die Constraints Ungleichungen sind, wird der Lösungsraum durch die Fläche der sich überlappenden Graphen gebildet. Projiziert auf die Achsen des Koordinatensystems, ergeben sich die gültigen Wertebereiche $I_1$ und $I_2$ für $v_1$ und $v_2$ bzgl. der vorhandenen Constraints. In 5.27(b) ist zu sehen, wie der Lösungsraum von $R_{1,2}$ durch eine hierarchische, binäre Zerlegung der Wertebereiche approximiert werden kann, und dies in 5.27(c) zu einem Quartärbaum (engl. quadtree) $T_{1,2}$ führt.^5.110

Abbildung 5.27: Beispiel für die Generierung eines $2^k$-Baums (vgl. Haroud und Faltings, 1994, S. 41 ff.)

Die entstehenden $2^k$-Bäume $T_{i,j}$ repräsentieren jeweils die Relationen $R_{i,j}$. Auf ihnen können Weiterentwicklungen des Waltz-Filteralgorithmus zur Herstellung von Kantenkonsistenz, Pfadkonsistenz, etc. angewendet werden. In bestimmten Fällen, für konvexe, binäre Constraints, führt Pfadkonsistenz innerhalb polynomialer Laufzeitkomplexität gleichzeitig zu globaler Konsistenz.^5.111 Pfadkonsistenz wird durch die in Abschnitt 5.2.3.4 f. beschriebenen Operationen composition und intersection erreicht. Sam-Haroud und Faltings (1996a, S. 98) stellen dies wie folgt dar:

$$T'_{i,j} = T_{i,j} \oplus \prod_{i,j}^{}{(T_{i,k} \otimes T_{k,k} \otimes T_{k,j})}$$

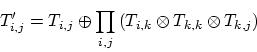
Ebenso kann bei Bedarf niedrigere Konsistenz hergestellt werden. Da Pfadkonsistenz eine Generalisierung der Kantenkonsistenz ist, kann analog Kantenkonsistenz folgendermaßen erreicht werden:

$$T'_{i,i} = T_{i,i} \oplus \prod_{i}^{}{(T_{i,j} \otimes T_{j,j})}$$

Während die intersection-Operation $\oplus$ die Überschneidung der Wertebereiche impliziert, was sich innerhalb der $2^k$-Baum-Repräsentation wiederum problemlos durch Bildung der logischen Schnittmenge der betreffenden Bäume durchführen lässt, muss zur Bestimmung der ,,Pfade`` im Constraint-Netz durch die composition-Operation $\otimes$ eine komplexere Umwandlung vorgenommen werden. Anstatt die composition, wie bei den klassischen Pfadkonsistenz-Algorithmen, durch binäre Matrizen-Multiplikation zu berechnen, werden in Bezug auf $2^k$-Bäume die k-dimensionalen Constraints durch die Projektion $\prod$ in den (k+1)-dimensionalen Raum und wieder zurück in die k-te Dimension projiziert. Die Regeln dieser Projektionen führen in diesem Fall zur Realisierung des composition-Operators. Gegeben die Ordnung $wei{\textit{\ss{}}} < grau < schwarz$ sind die folgenden Regeln anzuwenden (vgl. Sam-Haroud und Faltings, 1996a, S. 98):

i.

$color(node_1 \oplus node_2) = Max(color(node_1), color(node_2))$

ii.

$color(node_1 \otimes node_2) = Max(color(node_1), color(node_2))$

iii.

$color(\prod{(node)}) = Min(color(node_i))$
wobei $node_i$ alle Knoten sind, die $\prod{(node)}$ als Facette besitzen

In Abbildung 5.28 ist ein Würfel zu sehen, dessen 3-dimensionale Knoten aus deren 2-dimensionalen Facetten abgeleitet werden können. Umgedreht ist es möglich, Informationen über eine Facette zu erhalten, indem die 3-dimensionale Ausprägung über eine ihrer Facetten projiziert wird. Die Operatoren zur Herstellung von Kantenkonsistenz, Pfadkonsistenz und weiteren Generalisierungen benötigen somit ausschließlich logische anstatt numerische Operationen zu ihrer Durchführung vgl. Haroud und Faltings, 1994, S. 43; Sam-Haroud und Faltings, 1996a, S. 98.

Abbildung 5.28: Projektion von Facetten (vgl. Sam-Haroud und Faltings, 1996a, S. 97)

Fußnoten

...^5.110

$2^k$-Bäume: binäre Relationen führen zu Quartärbäumen, ternäre Relationen zu Oktärbäumen (engl. octree), usf. vgl. Haroud und Faltings, 1994, S. 42; Sam-Haroud und Faltings, 1996a, S. 93

...^5.111

Analog strenge $5$-Konsistenz für konvexe, ternäre Constraints.