![\begin{figure}\centering
\includegraphics[width=12.5cm]{images/constraints_pc_beispiel}
\ifx\pdfoutput\undefined
\fi
\end{figure}](img145.png) |
Da Kantenkonsistenz nicht alle inkonsistenten Werte aus den Domänen der Constraint-Variablen ausschließt, und zudem nicht sichergestellt ist, dass ein kantenkonsistentes Constraint-Netz eine Lösung besitzt, wurden höhere Konsistenzgrade und Verfahren zu deren Herstellung entwickelt. Die natürliche Erweiterung der Kantenkonsistenz ist die Pfadkonsistenz. Zur Herstellung der Pfadkonsistenz werden Pfade im Constraint-Graphen betrachtet, wobei ein Pfad eine Sequenz von Constraint-Variablen bzw. Knoten im Constraint-Netz ist.5.23 Dabei werden wie bei der Kantenkonsistenz Wertebelegungen eliminiert, die im Widerspruch zu den durch die Constraints formulierten Forderungen stehen.
Allgemein formuliert: Ein Pfad
![]() in
einem Constraint-Graph ist pfadkonsistent, wenn sich für alle
Wertepaare für
in
einem Constraint-Graph ist pfadkonsistent, wenn sich für alle
Wertepaare für ![]() , die das binäre Constraint
, die das binäre Constraint ![]() erfüllen, Werte für die dazwischenliegenden Variablen
erfüllen, Werte für die dazwischenliegenden Variablen ![]() finden
lassen, so dass die entsprechenden Constraints
finden
lassen, so dass die entsprechenden Constraints
![]() entlang des Pfades erfüllt
sind (siehe Abbildung 5.8). Formal
kann dies wie folgt ausgedrückt werden
(vgl. Mackworth, 1977a, S. 103):
entlang des Pfades erfüllt
sind (siehe Abbildung 5.8). Formal
kann dies wie folgt ausgedrückt werden
(vgl. Mackworth, 1977a, S. 103):
Ein Constraint-Netz ist pfadkonsistent, wenn alle Pfade im
Constraint-Graph pfadkonsistent sind. Zu beachten ist, dass die
Definition von Pfadkonsistenz für einen Pfad
![]() nicht bedingt, dass konsistente
Wertebelegungen für diese Variablen konsistent sind mit Constraints,
die nicht Teil dieses Pfades sind. Es wird also wiederum lediglich
eine lokale Konsistenz erreicht.
nicht bedingt, dass konsistente
Wertebelegungen für diese Variablen konsistent sind mit Constraints,
die nicht Teil dieses Pfades sind. Es wird also wiederum lediglich
eine lokale Konsistenz erreicht.
In (Montanari, 1974) weist Ugo Montanari nach, dass Pfadkonsistenz für vollständige Constraint-Graphen erreicht werden kann, indem sichergestellt wird, dass alle Pfade der Länge zwei pfadkonsistent sind (vgl. Mackworth, 1977a, S. 111). Es reicht daher aus, innerhalb eines vollständigen Constraint-Netzes die Konsistenz für Wertetripel, d.h. für alle Pfade der Länge zwei, sicherzustellen, damit das gesamte CSP pfadkonsistent ist.5.24 Verkürzt lässt sich daher Pfadkonsistenz auch wie folgt definieren (vgl. Mackworth, 1977a, S. 100 f.):
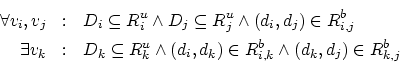
Zur Repräsentation der Abhängigkeiten nutzen
Pfadkonsistenz-Algorithmen eine extensionale
Darstellung in Form von booleschen Matrizen. Voraussetzung hierfür
ist, dass für die Wertebereiche der Constraint-Variablen eine fixe
Reihenfolge angenommen wird. Binäre Constraints lassen sich mittels
Matrizen darstellen, indem jeder Eintrag einer Matrix für eine
konsistente oder inkonsistente Wertekombination der beiden beteiligten
Variablen steht. Ein Constraint ![]() , welches die Ungleichheit
von
, welches die Ungleichheit
von ![]() spezifiziert, wobei die beiden identischen Domänen
spezifiziert, wobei die beiden identischen Domänen
![]() und
und
![]() jeweils nur zwei Werte enthalten,
wird z.B. durch die folgende Matrix repräsentiert:
jeweils nur zwei Werte enthalten,
wird z.B. durch die folgende Matrix repräsentiert:
![\begin{displaymath}
C_{i,j} =
\left[
\begin{array}{c c}
0 & 1 \\
1 & 0 \\
\e...
...1 & 2 \\ \hline
1 & 0 & 1 \\
2 & 1 & 0 \\
\end{array}\right]
\end{displaymath}](img167.png)
Aus Gründen der Einheitlichkeit und Vereinfachung werden die Domäne
einer Variablen und unäre Constraints in dieser Repräsentation als
binäres Constraint ![]() dargestellt, wobei dazu auf der
Diagonalen der Matrix jeweils der Wert 1 eingetragen wird. Der
Wertebereich
dargestellt, wobei dazu auf der
Diagonalen der Matrix jeweils der Wert 1 eingetragen wird. Der
Wertebereich
![]() einer Variable
einer Variable ![]() wird demnach
z.B. durch die folgende Matrix repräsentiert:
wird demnach
z.B. durch die folgende Matrix repräsentiert:
![\begin{displaymath}
C_{i,i} =
\left[
\begin{array}{c c c}
1 & 0 & 0 \\
0 & 1 ...
...& 0 \\
4 & 0 & 1 & 0 \\
5 & 0 & 0 & 1 \\
\end{array}\right]
\end{displaymath}](img173.png)
![\begin{displaymath}
C_{i,i} =
\left[
\begin{array}{c c c}
1 & 0 & 0 \\
0 & 1 ...
...& 0 \\
4 & 0 & 1 & 0 \\
5 & 0 & 0 & 0 \\
\end{array}\right]
\end{displaymath}](img174.png)
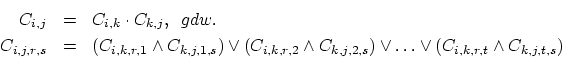
Wobei ![]() die
die ![]() -te Zeile,
-te Zeile, ![]() die
die ![]() -te Spalte und
-te Spalte und ![]() die
Kardinalität von
die
Kardinalität von ![]() bezeichnet. Ein Beispiel für eine derartige
Operation:
bezeichnet. Ein Beispiel für eine derartige
Operation:
![\begin{displaymath}
\left[
\begin{array}{c c c}
1 & 0 & 1 \\
0 & 1 & 0 \\
1...
...0 & 1 & 0 \\
1 & 1 & 1 \\
0 & 1 & 0 \\
\end{array}\right]
\end{displaymath}](img182.png)
Wie AC-1 ist der Algorithmus
PC-1 sehr ineffizient, da für jede Änderung an
nur einem einzigen Constraint der Algorithmus komplett erneut
durchlaufen werden muss. Aufgrund der vielen Variablen ![]() ist
PC-1 zudem sehr speicherintensiv. Der
Algorithmus PC-2
(vgl. Mackworth, 1977a, S. 113) ist ähnlich wie
AC-3 eine Verbesserung in der Hinsicht, dass
bei Änderungen nur noch die betroffenen Constraints erneut geprüft
werden müssen.
ist
PC-1 zudem sehr speicherintensiv. Der
Algorithmus PC-2
(vgl. Mackworth, 1977a, S. 113) ist ähnlich wie
AC-3 eine Verbesserung in der Hinsicht, dass
bei Änderungen nur noch die betroffenen Constraints erneut geprüft
werden müssen.
Neben PC-1 und PC-2 gibt es noch eine Reihe weiterer, bekannter Pfadkonsistenz-Algorithmen. Sie sind jeweils Verallgemeinerungen der entsprechenden Algorithmen zur Herstellung von Kantenkonsistenz. So ist der Algorithmus PC-3 eine Verbesserung von PC-2, der seine erhöhte Effizienz mit ähnlichen Mechanismen und denselben Nachteilen bzgl. erhöhtem Speicherbedarf zur Verwaltung von zusätzlichen Informationen erreicht, wie AC-4 gegenüber AC-3. PC-3 wird zusammen mit AC-4 von Mohr und Henderson (1986) vorgestellt. Aufgrund kleinerer Fehler in PC-3 präsentierten Ching-Chih Han und Chia-Hoang Lee eine korrigierte Version namens PC-4 (vgl. Han und Lee, 1988).5.29 Die Algorithmen PC-5 und PC-5++ von Moninder Singh sind weitere Verbesserungen, basierend auf AC-6 bzw. AC-6++ (vgl. Singh, 1995). Hauptvorteil ist die geringere Platzkomplexität der Algorithmen, wobei die worst-case Zeitkomplexität gleich der von PC-4 ist. Das durchschnittliche Laufzeitverhalten ist jedoch deutlich verbessert.
Unabhängig von PC-5 wurde der Algorithmus PC-6 entwickelt, der ebenfalls das Prinzip des minimal support von AC-6 auf die Pfadkonsistenz überträgt (vgl. Chmeiss und Jégou, 1995; Chmeiss, 1996)5.30. Die Algorithmen bzw. deren Eigenschaften sind demnach identisch. Die Algorithmen PC-7 (vgl. Chmeiss und Jégou, 1996a) und PC-8 (vgl. Chmeiss und Jégou, 1998,1996b) von Assef Chmeiss und Philippe Jégou basieren ebenfalls wie PC-5 bzw. PC-6 darauf, nicht benötigte Konsistenzberechnungen durch minimal support zu vermeiden, allerdings ohne diese supports in einer aufwendigen Datenstruktur zu speichern. Der Algorithmus PC-8 ist dabei als eine Optimierung von PC-7 hinsichtlich der Platzkomplexität zu sehen. Einer Verbesserung des Speicherbedarfs steht bei beiden Algorithmen eine leichte Verschlechterung des Laufzeitverhaltens gegenüber. Eine Übersicht über die jeweiligen worst-case Zeit- und Platzkomplexitäten der hier angesprochenen Algorithmen befindet sich in der Tabelle 5.1.
Obwohl die Pfadkonsistenz einen höheren Konsistenzgrad darstellt als die Kantenkonsistenz und ggf. wesentlich mehr Werte aus den Wertebereichen der Variablen eines CSP entfernt, die nicht Teil einer Lösung sein können, werden die entsprechenden Algorithmen zum Herstellen von Pfadkonsistenz, außer bei speziellen Problemstellungen, relativ selten eingesetzt. Dies liegt darin begründet, dass Pfadkonsistenz mehrere Probleme mit sich bringt (vgl. Barták, 2001, S. 10): So filtern Pfadkonsistenz-Algorithmen zwar mehr inkonsistente Werte aus den Wertebereichen heraus, allerdings wird dafür im Vergleich zur Kantenkonsistenz ein wesentlich schlechteres Verhältnis in Bezug zur Ausführungsgeschwindigkeit bzw. Zeitkomplexität in Kauf genommen. Weiterhin ist der Speicherbedarf von Pfadkonsistenz-Algorithmen durch die extensionale Repräsentation aller Constraints bzw. Domänen auch für überschaubare Problemstellungen wesentlicher höher als bei Verfahren zur Herstellung von Kantenkonsistenz. Zudem werden bei der Herstellung von Pfadkonsistenz abgeleitete Constraints zu dem Constraint-Netz hinzugefügt. Suchverfahren zur Bestimmung von Lösungen, die bestimmte, vormals vorhandene Strukturen eines Constraint-Netzes ausnutzen, lassen sich dadurch nicht mehr anwenden. Und letztendlich stellt Pfadkonsistenz i.A. immer noch lediglich lokale Konsistenz her, d.h. es werden nicht alle inkonsistenten Werte aus den Domänen entfernt.
Eine besondere Rolle bzgl. Pfadkonsistenz spielen allerdings sog. row-convex-Constraints. Ein binäres Constraint in Matrixrepräsentation ist row-convex, wenn in jeder Zeile der Matrix die 1er Einträge aufeinander folgend sind und nicht durch eine 0 in derselben Zeile unterbrochen werden. Für diese Art Constraints wird von van Beek (1992) nachgewiesen, dass Pfadkonsistenz gleichbedeutend mit globaler Konsistenz ist. Die Konvexitätseigenschaften haben eine besondere Relevanz z.B. für Zeitplanungsprobleme formalisiert durch TCSPs (vgl. Abschnitt 4.4.1) und bei Verfahren zum Auffinden von Lösungen in ICSPs (vgl. Abschnitt 5.3.1.4 und Abschnitt 5.3.7).